Estudio electromagnético de las pastillas de guitarra eléctrica

Bobinado en serio o en paralelo

Cuando los componentes están unidos uno tras otro, es decir, que la corriente tiene atravesar un componente para llegar al siguiente se dice que están la conexión es en serie. Por el contrario, si “comparten extremos”, si la corriente se puede dividir de tal manera que parte de la corriente atraviese un componente y que otra parte atraviesa el otro se dice que están conectados en paralelo

 

 

 

 

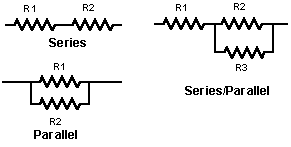
En una guitarra Stratocaster, recién salida de la fábrica, las pastillas están colocadas en paralelo en la posición 2 (mástil y medio) y en la posición 4 (puente y medio). Vamos a estudiar cuales son las características que diferencian la colocación de unas pastillas en serie o paralelo.

Las pastillas tienen normalmente una impedancia de 4 a 10 kohms. Cuando están en paralelo la impedancia se reduce considerablemente. Esto es provocado porque una peque a impedancia inductiva de cada pastilla se carga en la otra pastilla. Cada pastilla funciona, en resumen, como un filtro paso-alto básico entre la otra pastilla y el salida. En cambio, cuando las pastillas están en series, no se produce este efecto de filtrado ya que la impedancia se suma.

También varia notablemente la potencia de salida del dispositivo. La salida siempre es más fuerte cuando las pastillas están colocadas en serie, esto es debido, como en el caso anterior, a que no existe realimentación entre las pastillas.

La inductancia efectiva de dos bobinas es muy distinta si están conectadas en serie o si están conectadas en paralelo. Esto afecta directamente a la respuesta en frecuencia que depende de la inductancia.

La inductancia, que se mide en henrios (o milihenrios, mh), es la magnitud con la que se define a las bobinas, para calcular la inductancia total, para explicarlo vamos a suponer dos bobinas de 10mh:

En serie: la inductancia total es la suma 10mh + 10mh = 20mh.

En paralelo: el total es el producto dividido la suma (10mh X 10mh) / (10mh + 10mh) = 100mh / 20mh= 5mh.

 

Análisis en frecuencia de una pastilla

En este apartado vamos a analizar desde un punto de vista eléctrico la respuesta en frecuencia de las pastillas de una guitarra eléctrica. Para ello lo que tenemos que hacer primeramente es analizar el circuito equivalente de una pastilla. Luego a partir de el podremos deducir ciertas características del sonido que tendrá cada pastilla. La utilización de un circuito equivalente supone una simplificación del problema que nos permite hacer cuentas a costa de perder la fiabilidad absoluta. En nuestro caso con este circuito podremos observar los efectos mas importantes producidos por las pastillas aunque habrá otros efectos mas complejos que no se podrán explicar de esta manera.

Circuito equivalente de una pastillas

Desde un punto de vista eléctrico, una pastilla magnética es equivalente a este circuito.

 

 

 

 

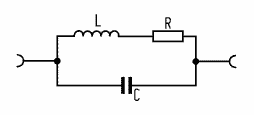
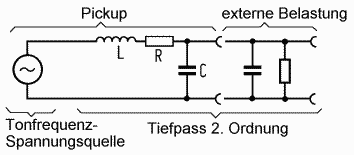
Una bobina real puede ser descrita eléctricamente como una inductancia (L) ideal en serie con una resistencia (R), y en paralelo a estos una capacidad (C). Lo mas importante en este circuito con diferencia es la cantidad de inductancia, que depende en el numero de vueltas, el material magnético del nucleo de la bobina y la geometría de la pastilla. La resistencia y la capacidad no tienen mucha influencia y pueden ser despreciadas. Cuando las cuerdas se mueven se induce un voltaje AC en la bobina. Así que la pastilla actúa como una fuente de alterna con unos componentes electrónicos unidos.

 

 

 

 

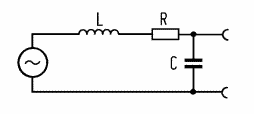
La carga externa consiste en una resistencia (los potenciómetros del tono y volumen, y cualquier resistencia de entrada del amplificador) y una capacidad parasita debida al cable y las uniones. Este conjunto de componentes pasivos forma un filtro paso-bajo de segundo orden.

 

 

 

 

 

 

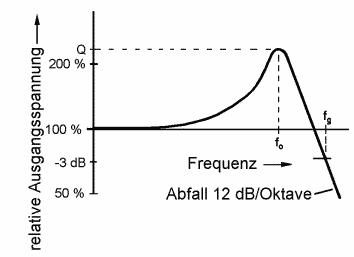
Como cualquier otro filtro similar, tiene una frecuencia de corte fg, que es donde la respuesta baja 3dB (mitad de la potencia). Por encima de fg, la respuesta decae a un ritmo de 12dB por octava. No hay descenso de potencia a bajas frecuencias aunque un poco por debajo de la frecuencia fg (fcero) ser produce una resonancia entre la inductancia de la pastilla y la capacidad del cable de la guitarra. Esta frecuencia, llamada fcero, proporciona la máxima amplitud de pico. El filtro paso-bajo pasivo funciona como un amplificador de voltaje en esa zona (pero no amplifica la potencia porque la impedancia de salida se hace muy alta a la vez.

 

 

 

 

Si uno sabe la frecuencia de resonancia y la amplitud de pico, conoce aproximadamente el 90% de la característica de transferencia de la pastilla. Estos par metros son la clave del sonido de una pastilla (con este modelo hay otros efectos que no pueden ser descritos pero su influencia no es tan importante).

 

-Podemos resumir lo que suceder con los armónicos de la siguiente forma:

Los armónicos por encima de la frecuencia de resonancia serán progresivamente atenuados.

Los armónicos en el rango de frecuencias de la resonancia serán amplificados.

Los armónicos y tonos fundamentales por debajo de la frecuencia de resonancia serán reproducidos sin alteración.

 

Como la Resonancia Afecta al Sonido

La frecuencia de resonancia de la mayor a de las pastillas en combinación con cables normales se encuentran entre 2000 y 5000 Hz. Este es el rango donde el o do humano es mas sensible. El resultado de la colocación de la frecuencia de resonancia es, subjetivamente, un sonido:

2000 Hz: cálido y suave

3000 Hz: brillante y con presencia

4000 Hz: penetrante

5000 Hz: quebradizo y pobre

El sonido también depende de la altura del pico. Un pico elevado produce un sonido potente y característico. Mientras que un pico suave produce un sonido mas débil, especialmente en las guitarras de cuerpo solido que no tienen caja de resonancia. La altura del pico de la mayor parte de las pastillas del mercado oscila entre 1 y 4 (0 a 12 dB), depende de material de la bobina, de la resistencia de carga.

La frecuencia de resonancia depende de la inductancia L (entre 1 y 10 Henrios) y de la capacitancia C que es la suma de la de la pastilla (80-200pF) y la del cable (500-1000pF). Se puede ver como cambiando el cable que une la guitarra con el amplificador podemos variar su capacidad y por tanto la frecuencia de resonancia.

—————————————————————————————–

Estudio Electromagnético

 

En este apartado vamos a seguir un estudio electromagnético para llegar a un resultado que explique la transformación del movimiento de una cuerda de la guitarra eléctrica en un voltaje variable que equivale al sonido electrificado de la guitarra. Para ello vamos a ir avanzando poco a poco en el planteamiento siguiendo los siguientes puntos:

 

1. Esquema de una pastilla

2. Las propiedades magnéticas del flujo y los materiales ferromagnéticos

3. La creación de campos magnéticos variables debido a las vibraciones de las cuerdas.

4. La inducción de un voltaje debido al cambio del flujo magnético.

5. Las ecuaciones de Maxwell que describen las pastillas de la guitarra eléctrica.

 

Esquema de una pastilla

 

 

 

 

 

 

 

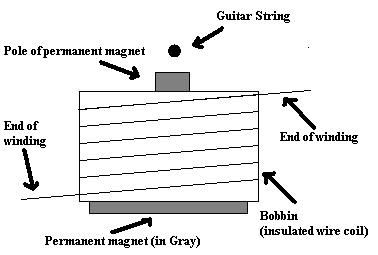
Cada pastilla mide unos 2 ” de largo y ” de ancho y consiste en un imán permanente que tiene un cable enrollado llamado bobina. Además, el imán permanente tiene seis “salientes” que sobresalen de la bobina, cada uno de ellos correspondiente a una cuerda de la guitarra. La pastilla está colocada en el cuerpo de la guitarra alineada de tal forma que cada “saliente” de la pieza está colocado exactamente debajo de su cuerda correspondiente.

 

Este es el esquema de pastilla que vamos a utilizar a lo largo de todo el estudio. Excluimos las pastillas humbucker que al tener dos bobinas poseen interacciones distintas a las de este sistema. Mas adelante para simplificar las formulas solo tendremos en cuenta un núcleo magnético y una sola cuerda.

 

2. Las propiedades magnéticas del flujo y los materiales ferromagnéticos

 

El primer objetivo de la pastilla de la guitarra eléctrica es convertir las oscilaciones de una cuerda en variaciones del flujo magnético (se define como la cantidad de intensidad magnética que atraviesa una superficie, como dice la ecuación ).

 

 

 

 

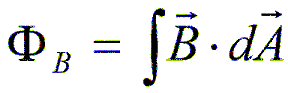
Este flujo magnético es necesario cuando calculamos el campo electromagnético inducido en la bobina. El flujo magnético puede ser cambiado de dos maneras. Cambiando la intensidad del campo, o cambiando el tamaño del rea. En nuestro caso el tamaño de la bobina es fijo luego la única manera que tendremos de cambiar el flujo ser variando la intensidad del campo magnético.

 

El movimiento de la cuerda de la guitarra cambia el campo magnético de la bobina. Una cuerda de guitarra esta hecha de acero, que es un material ferromagnético . Un material ferromagnético no tiene un campo magnético inherente, pero tiene gran facilidad para realzar cualquier campo en el que están situados. Este fenómeno es debido a que pequeñas áreas de estos materiales son magnéticas. Como la orientación de dichas regiones magnéticas es aleatoria, los momentos magnéticos se cancelas, y el material como un todo no es magnético. Pero cuando existe un campo magnético externo, estos momentos tienden a alinearse y producen un campo magnético propio que se añade al campo magnético existente. Los materiales ferromagnéticos permaneces magnetizados incluso después de que el campo externo haya desaparecido.

 

 

 

 

 

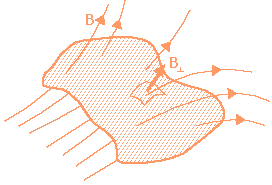
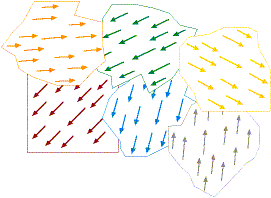
Regiones magnéticas aleatorias en un material Ferromagnético

 

 

 

3. La creación de campos magnéticos variables debido a las vibraciones de las cuerdas.

Los materiales ferromagnéticos pueden ser utilizados para realzar los campos magnéticos. Los solenoides utilizan este principio para crear unos campos magnéticos mayores para una misma cantidad de energía. De la teoría magnética sabemos que el campo magnético de un solenoide depende solamente de de la constante de permeabilidad, como se puede ver en la ecuación, de la intensidad ( i ) y del n mero de vueltas por unidad de longitud ( n ). La manera más económica de incrementar el campo magnético es cambiar la constante de permeabilidad. La solución para esto es introducir un material en el centro del solenoide que incrementa esta constante, creando un campo magnético mucho mayor. Este efecto es similar al que se puede observar en las pastillas de una guitarra eléctrica.

 

 

 

 

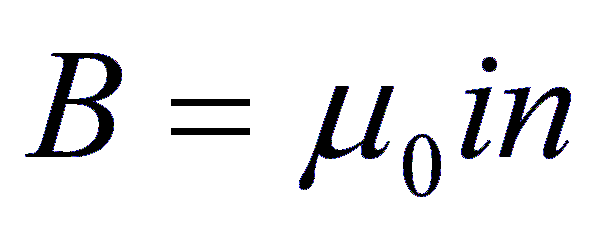
Antes de comenzar a tocar, cuando las cuerdas están en reposo, la pastilla magnética induce un campo magnético en la cuerda de la guitarra. Este aumenta el tamaño del campo magnético, que incrementa a su vez el flujo a través de la bobina. Cuando la cuerda es pulsada, el flujo a través de la bobina varia en función de la distancia de la pastilla a la cuerda. Cuando la distancia es menor, el campo magnético efectivo es mayor, y el flujo es mayor, y viceversa. La frecuencia de la variación depende exclusivamente en el movimiento de la cuerda.

 

Cuando una cuerda es pulsada, se mueve de una manera oscilatoria. La frecuencia depende solamente del materia, la longitud y la tensión de la cuerda. Estas oscilaciones se producen en dos sentidos: arriba-abajo y izquierda-derecha con respecto a la bobina y el sonido se produce por la suma de ambas oscilaciones. Si las cuerdas solo se movieran arriba-abajo, el campo incrementar a y decrecer a una ver por cada periodo de la cuerda. En cambio si el movimiento es izquierda-derecha la frecuencia es del doble con respecto a la cuerda. Como la oscilación de la cuerda siempre es una combinación de ambos, el periodo del flujo magnético es mucho más complicado que un múltiplo simple del periodo de la cuerda.

 

En estas dos animaciones podemos observar como fluctúan los campos dependiendo del movimiento de la cuerda. El imán inferior representa la pastilla mientras que la circunferencia superior ser a la cuerda hecha de un material electromagnético.

 

 

 

 

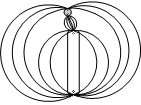
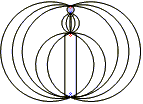
A la izquierda el movimiento es horizontal y a la derecha el movimiento es vertical.

 

4. La inducción de un voltaje debido al cambio del flujo magnético.

 

El siguiente paso que tenemos que estudiar es como transforma la pastilla el flujo magnético en corriente a través de la bobina. El procedimiento esta descrito seg n la Ley de Faraday. Esta Ley dice que una variación del flujo magnético produce un campo eléctrico contrario a la fuerza que lo crea. Cuando el material magnético se acerca a un aro de cable un flujo es creado. La dependencia matemática la expuesta en la ecuación de la derecha.

 

 

 

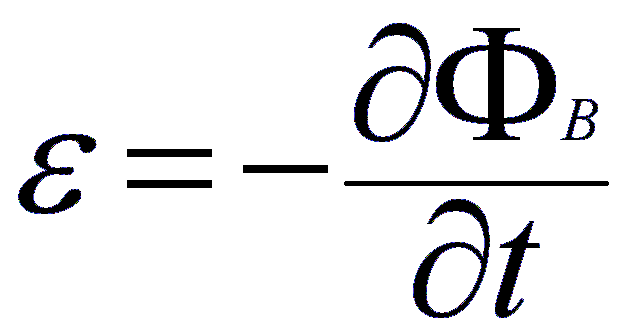
A partir de esta Ley es fácil suponer el funcionamiento de una pastilla. La cuerda ferromagnética produce unas variaciones de flujo que dependen en el tiempo de manera sinusoidal, lo que produce un campo eléctrico en la bobina.

 

5. Las ecuaciones de Maxwell que describen las pastillas de la guitarra eléctrica.

La física que hay detrás de una pastilla de la guitarra eléctrica puede ser analizada utilizando las ecuaciones de Maxwell. El dispositivo puede ser simulado por un simple solenoide; el núcleo hecho de hierro y el cable exterior hecho de cobre. La idea es que la cuerda sobre el núcleo magnético vibra y causa un variación en la campo magnético producido por el núcleo. Esta variación es “notada” por el cable y como resultado se produce un campo eléctrico en la bobina. Todo el sistema puede ser resuelto usando la segunda ecuación de Maxwell y el teorema de Stoke.

 

 

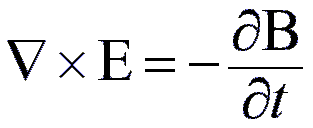
Segunda ecuación de Maxwell

 

 

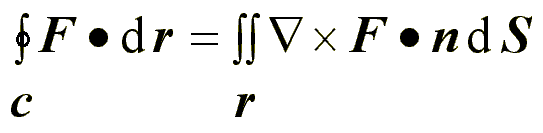
Teorema de Stoke

 

Utilizando la ecuación anterior vamos a ser capaces de evaluar y analizar la pastilla de la guitarra eléctrica. Primero, vamos a simplificar nuestro estudio reduciendo la pastilla a una bobina con un núcleo magnético. En la realidad hay tantos núcleos como cuerdas pero por simplicidad centraremos nuestro estudio a una sola. Por encima de la bobina hay hilo ferromagnético, como níquel o hierro.

 

 

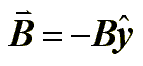
Modelaremos la vibración de la cuerda sobre el imán como un movimiento circular y asumimos que el espacio entre los dos es despreciable. Sabemos que el campo magnético en un cable magnético viene dado por:

 

El campo magnético puede ser estimado, teniendo en cuenta que lo consideramos un movimiento circular, como:

 

 

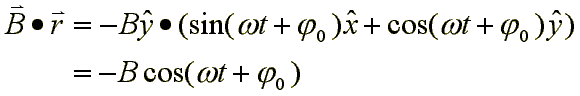
Donde omega es la frecuencia, medida en rad/s, a la que vibra al cuerda sobre el núcleo

Gracias a la aproximación que hemos asumido de que la distancia entre ellos es suficientemente peque a, podemos ignorar las atenuaciones de la onda. El campo total con el que nos encontramos vendrá dado por la suma del producido por la cuerda más el producido por el núcleo. Luego:

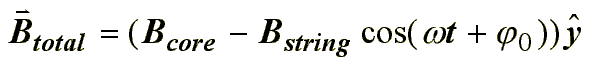
Luego aplicamos las ecuaciones de Maxwell y integramos ambos miembros de la ecuación.

 

 

 

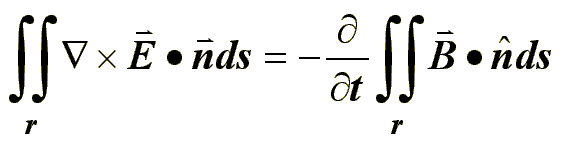
Luego aplicamos el teorema de Stokes para eliminar el rotacional del campo eléctrico:

 

 

 

 

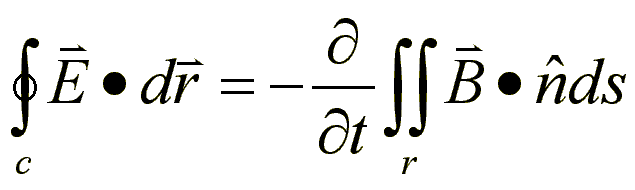
Por último obtenemos la solución, es decir, el valor del campo eléctrico en función del magnético:

 

 

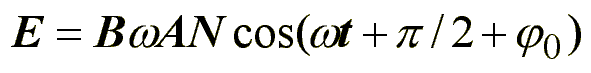
Este es campo magnético producido por el flujo magnético que se produce en la bobina debido a las vibraciones de la cuerda. B es el campo magnético en la cuerda, A es el rea de la bobina y N es el número de cuerdas en el cable. Como se puede ver en esta ecuación, la magnitud del campo eléctrico es directamente proporcional a la frecuencia del estímulo. Además, la frecuencia con la que vibra la cuerda es también la frecuencia del campo eléctrico. También se ve claramente como lo que se obtiene a la salida es una se al alterna (AC) sin ninguna componente continua como ya habíamos supuesto en otros apartados.

 

 

http://www.lpi.tel.uva.es/~nacho/